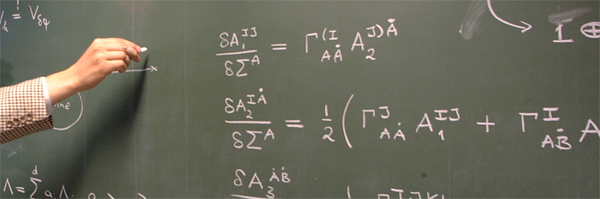
Quantum Gravity and Unified Theories
This department attends to the development of a theory that unifies quantum theory and general relativity – in the framework of superstring theory as well as canonical quantization.
Despite intense efforts over the last years it is far from clear at this time what a consistent theory of quantum gravity will look like and what its main features will be. In view of these uncertainties, the best strategy appears to be one which is both diversified and interdisciplinary. For this reason, the department aims to represent all the major current approaches to quantum gravity, in particular supergravity and string theory and their modern developments, as well as other approaches.
Canonical approaches to quantum gravity traditionally emphasize the geometrical aspects and appear well suited to deal with unsolved conceptual issues of quantum gravity, such as e.g. the problem of time or the interpretation of the wave function of the universe. More recently, these insights have been combined with the study of hidden algebraic structures underlying the equations governing gravity to deepen our understanding of situations where classical general relativity breaks down, such as the study of cosmological or black hole singularities.
String theory, on the other hand, takes a very different point of departure in tackling the problem of quantum gravity. The requirement of mathematical consistency and the non-renormalizability of perturbatively quantized gravity, and the need to incorporate the non-gravitational interactions are likely to force us to modify Einstein's theory at the smallest distances (Planck scale). This may not only lead to a geometrization of the other fundamental forces (as exemplified by Kaluza-Klein theories and supergravity) and the unification of matter and gravity, but to an entirely new type of theory, which could explain how space-time is dissolved at very small distances, and in which Einstein's theory emerges only as an effective low energy theory, valid above distances above the Planck scale. Superstring and supermembrane theory, and supersymmetric matrix theory are the most promising ansaetze so far in this direction. Major progress in this area has been recently achieved by members of the department, in particular the framework of the so-called AdS/CFT correspondence, and the study of certain infinite dimensional symmetries, which might underlie a unified and non-perturbative description of string theory (M theory).

