Theoretische Dynamik der Gravitation und Strahlung

Seit mehr als einem Jahrhundert ist Einsteins Allgemeine Relativitätstheorie (ART) unsere beste Beschreibung der Gravitation. Einerseits beschreibt sie Newtons Theorie der Gravitation im Grenzfall schwacher Felder und langsamer Bewegung und damit die alltägliche Gravitationsphysik auf der Erde und im Sonnensystem. Sie beschreibt aber auch die kleinen Abweichungen von der Newtonschen Gravitation, die bei Präzisionsmessungen im Sonnensystem beobachtet werden. Andererseits macht die ART exotische Voraussagen im Bereich starker Gravitationsfelder, wie z.B. die Existenz Schwarzer Löcher (SL) und dass alle sich umkreisenden Körper Gravitationswellen (GW) aussenden, was dazu führt, dass sie sich annähern und schließlich (andere Einflüsse ausgeschlossen) mit einander verschmelzen.

Die Existenz von Gravitationswellen wurde durch Beobachtung von Binärpulsaren in unserer Milchstraße bewiesen, deren Umlaufbahnen sich durch GW annähern. Allerdings bewegen sich diese Pulsare mit Geschwindigkeiten, die wesentlich kleiner sind als die Lichtgeschwindigkeit, so dass es hunderttausende von Jahren dauert bis sie verschmelzen.

Unsere ersten wirklichen Tests der exotischen Bereiche starker Gravitationsfelder begannen 2015 mit der ersten direkten Beobachtung von Gravitationswellen mit dem Laser Interferometer Gravitational-Wave Observatory (LIGO). Das erste durch die Erde gelaufene GW-Signal im Jahr 2015 rührte von der Umkreisung und der Verschmelzung zweier Schwarzer Löcher her. Seitdem wurden mehrere SL-Doppelsysteme nachgewiesen, und im Jahr 2017 wurde die erste Neutronenstern-Verschmelzung beobachtet.

Diese Beobachtungen stellen den Beginn des Zeitalters der Gravitationswellen-Astronomie dar. Die Analyse der Signale hat unsere Vorstellungen von der Natur der GW bisher bestätigt - aber dies ist erst der Anfang der wissenschaftlichen Möglichkeiten für LIGO und die anderen Gravitationswellen-Observatorien. Die nächsten Ausbaustufen von LIGO und Virgo versprechen weit höhere Signal-zu-Rausch-Verhältnisse, was (i) zu genaueren Tests der allgemeinen Relativitätstheorie führt und (ii) zu einer größeren Anzahl nachgewiesener Signale. Für Binärsysteme aus Neutronensternen muss man auch den Einfluss des inneren Aufbaus der Sterne berücksichtigen. In der Tat stellt die Aufstellung von Beschränkungen für die superdichte Materie von Neutronensternen eines der wichtigsten ungelösten Probleme der modernen Kernphysik dar. Die erste Beobachtung eines Neutronenstern-Binärsystems hat bereits zu Einschränkungen bezüglich der inneren Struktur der Sterne geführt, aber weit engere Beschränkungen werden bei zukünftigen Beobachtungen in den nächsten Jahren möglich sein.

Die Möglichkeit, Gravitationswellen-Signale nachzuweisen und daraus wissenschaftliche Folgerungen zu ziehen, erfordert detaillierte Modelle der Form des Signals. Für Binärsysteme aus Schwarzen Löchern bedeutet dies, die Voraussagen der allgemeinen Relativitätstheorie für die Eigenschaften und die Dynamik Schwarzer Löcher mit Leben zu erfüllen und mögliche Abweichungen von der ART zu berücksichtigen. Für Binärsysteme aus Neutronensternen muss man auch den Einfluss der noch immer unbekannten inneren Physik der Neutronensterne betrachten und zusätzlich die mit den gleichen Verfahren berechneten Einstein-Gleichungen für Schwarze Löcher, wie weiter unten beschrieben.

Binärsysteme aus Schwarzen Löchern

Schwarze Löcher sind Bereiche der Raumzeit, in denen die Materie so dicht geworden ist (z.B. nach dem Kollaps eines massiven Sterns), dass die Gravitation die Materie dazu bringt, hinter dem Ereignishorizont zu verschwinden, einer Oberfläche aus der nicht einmal Licht entkommen kann und in deren Nähe die Zeit fast still steht. Während die Astronomen zahlreiche dichte Objekte gefunden haben, die dieser Beschreibung entsprechen, steht ein konkreter Nachweis noch aus, dass Schwarze Löcher genau wie in der AR vorhergesagt existieren.

Die Entdeckung von Gravitationswellen aus Binärsystemen von Schwarzen Löchern hat unser Vertrauen in unser Verständnis von SL und der ART sehr verstärkt, aber ihr relativ geringes Signal-zu-Rausch-Verhältnis hat viele Fragen offen gelassen, die mit künftigen Beobachtungen geklärt werden sollen. Wie bei den ersten Beobachtungen müssen wir detaillierte Formen der GW-Signale von Binärsystemen vorwegnehmen und parametrisieren, so dass wir sie erkennen und interpretieren können, wenn sie eintreffen.

Im Fall zweier Schwarzer Löcher in einem Binärsystem kann nur die Allgemeine Relativitätstheorie definitive Vorhersagen für den Orbit und das GW Signal machen. Für den Fall, dass wir die Einstein Gleichungen lösen können wissen wir daher bereits im Vorfeld, wonach wir suchen müssen.Jedoch hat sich das Auffinden einer hinreichend genauen, allgemeinen und praktischen Lösung des relativistischen Zwei-Körper-Problems als sehr schwierig herausgestellt; dies beschäftigt momentan viele Physiker auf der ganzen Welt und auch in unserer Abteilung am AEI.

Das relativistische Zwei-Körper-Problem lösen

In der numerischen Relativität werden Supercomputer benutzt, um die Einstein-Gleichungen direkt zu lösen und man hat damit große Erfolge bei der Bestimmung der Entwicklung von Schwarzen Löchern mit nahezu gleicher Masse erzielt. Aber es bleibt schwierig, den ganzen Parameterraum abzudecken (die Anfangsmassen der SL, die Spins und Bahnparameter), da die Simulation für einen gegebenen Parametersatz Monate dauern kann und weil Simulationen immer noch Schwierigkeiten haben, die Extremwerte des Parameterraums zu erreichen. Erfolgreiche Modelle der Gravitationswellen von SL-Binärsystemen müssen daher sowohl Daten aus der numerischen Relativität berücksichtigen als auch analytische Näherungen der ART.

Das Zwei-Körper-Problem selbst ist geeignet für zwei sich ergänzende Ansätze durch analytische Berechnungen, die in zwei Grenzregionen des Parameterraums gültig sind: Im Grenzfall schwacher Gravitation und langsamer Bewegung reduziert sich die allgemeine Relativitätstheorie auf die Newtonsche Gravitation; wird diese Grenze überschritten führt das zur Post-Newtonschen (PN) Näherung. Wenn das eine Schwarze Loch viel größer als das andere ist, reduziert sich das Problem auf eine Testmasse, die einer Geodäte in der stationären Raumzeit des großen Schwarzen Lochs folgt; die Ausweitung über diese Grenze hinaus ergibt die Näherung extremer Massenverhältnisse (EMV). Der effektive Ein-Teilchen-Formalismus (englisch: effective-one-body (EOB) formalism) benutzt Informationen über das PN-Limit, das EMV-Limit und die numerische Relativität in dem Versuch, ein genaues Modell über den ganzen Parameterraum zur Verfügung zu stellen.

Die Post-Newtonsche Näherung

Die Post-Newtonsche (PN) Theorie ist eine systematische störungstheoretische Näherung der ART, gültig für schwache Felder und bei langsamer Bewegung. Sie wurde zuerst in den 1920iger und 1930iger Jahren entwickelt und für Punktmassen zu hohen Ordnungen iteriert. Die PN-Resultate haben ausgezeichnete Tests relativistischer Effekte im Sonnensystem und bei Binärpulsaren ermöglicht. Allerdings blieben die PN-Effekte höherer Ordnung, wie z.B. solche die mit den Spins der Körper zu tun haben, unvollständig. Mitglieder der ACR-Abteilung arbeiten daran, die Kenntnis der Spin-Effekte in der PN-Theorie durch eine Vielzahl von Methoden voranzubringen, die als unabhängige Überprüfungen dienen: (i) einer Formulierung in harmonischer Eichung, bei der die Lösungen der PN-Gleichungen direkt berechnet werden, durch iterative Lösungen für die Bewegung und für das Gravitationsfeld, (ii) einem Hamiltonschen Rahmen für den konservativen Abschnitt, und (iii) Methoden, die der effektiven Feldtheorie der konservativen Dynamik entlehnt sind, wo das Problem in Feynman-Diagramme aufgelöst wird, die effektiv berechnet werden können und die relevanten Beiträge zu jeder PN-Ordnung identifizieren. Die Forschenden verwenden Computer-Algebra-Pakete, um ihre Berechnungen durchführbar zu machen, aber sehr viel Arbeit wird auch rein analytisch getan. Die Ergebnisse dieser Anstrengungen haben zu neuen Einsichten in das Verhalten von Spin und Drehimpulsen während einer Binärumkreisung geliefert und unsere Modelle von physikalisch realistischen Binärsystemen wesentlich verbessert. 

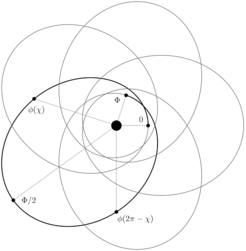
Die Näherung extremer Massenverhältnisse

In der EMV-Näherung wird die Lösung nullter Ordnung durch ein Testteilchen gegeben, das sich längs einer Geodäte durch den Hintergrund der Raumzeit eines Schwarzen Loches bewegt – die Schwarzschild-Raumzeit eines nicht rotierenden schwarzen Lochs oder die Kerr-Raumzeit eines rotierenden Schwarzen Lochs. Korrekturen zu dieser Lösung stammen sowohl aus „endliche Größe“-Effekten der Bewegung des leichteren Körpers (wegen seines Drehimpulses und vorhandenen oder erzeugten Deformationen) als auch von „Eigenkraft“-Effekten durch die Störung der Bewegung des leichten Körpers durch Rückwirkung auf das Gravitationsfeld. Die Berechnung von Eigenkraft-Effekten auf die Bewegung von Binärsystemen ist ein relativ neues, aber sehr aktives Studiengebiet, das analytische und numerische Techniken vereint. Das Verständnis des Zwei-Körper-Problems in der EMV-Näherung wird entscheidend bei der Analyse von Gravitationswellen sein, die aus der Verschmelzung von Objekten mit Sonnenmasse und supermassiven Schwarzen Löchern entstehen, und die von künftigen Detektoren im All – wie LISA – beobachtet werden können, aber auch für die Entwicklung von Modellen, die den gesamten Parameterraum beschreiben.

Die effektive Ein-Teilchen-Beschreibung

Der effektive Ein-Teilchen-Formalismus ist eine synergistische Näherung des Zwei-Teilchen-Problems, die Informationen aus dem PN-Limit, dem EMV-Limit und der numerischen Relativität zusammenführt, um eine genaue effektive Beschreibung der Bewegung zweier Teilchen durch den ganzen Parameterraum zu liefern. Die zentrale Idee dieses Modells besteht darin, die exakten Resultate für starke Felder aus dem Grenzfall rotierender Testmassen der Kerr-Raumzeit wiederzuerlangen, wobei alle bekannten Resultate der PN-Theorie für endliche Massenverhältnisse durch eine sorgsam gewählte Deformation der Kerr-Raumzeit vorgegeben sind. Die konservative Dynamik wird durch einen Hamilton-Operator beschrieben, der dann durch Strahlungsrückwirkungen, gekoppelt mit der Erzeugung von Wellenformen ergänzt wird. Das Modell ist flexibel genug, um mit Daten aus der numerischen Relativität kalibriert zu werden und liefert vollständige Wellenformen für die Annäherung, die Verschmelzung und das Abklingen des überbleibenden Schwarzen Loches.

Binärsysteme aus Neutronensternen

Neutronensterne stellen die extremsten Beispiele für gravitative, elektromagnetische und kernphysikalische Umgebungen dar, die stabil im Universum existieren. Sie bilden sich, wenn die entarteten Kerne von massiven Sternen in einer Supernova-Explosion kollabieren. Mehrere tausend Neutronensterne sind bis heute beobachtet worden; sie haben Massen vergleichbar mit der Sonnenmasse, aber alle Materie ist in einer Kugel von nur 10 km Radius enthalten, die mit bis zu 38000 Umdrehungen pro Minute rotiert. Die Magnetfelder sind bis zu hundert Billionen mal stärker als das Feld der Erde. Die Dichten im Innern von Neutronensternen sind so hoch, dass sie die mittlere Dichte von Atomkernen wohl übertreffen. Bei so extremen Dichten wird die Struktur der Kernmaterie, wie man sie aus der herkömmlichen Physik kennt, vollständig aufgelöst und statt dessen können völlig neue exotische Zustände der Materie entstehen. Die Bestimmung der Eigenschaften von solch ultradichter Materie wie z.B. ihre Zusammensetzung und Zustandsgleichung ist seit langem ein Ziel sowohl in der Grundlagenphysik als auch in der Astrophysik.

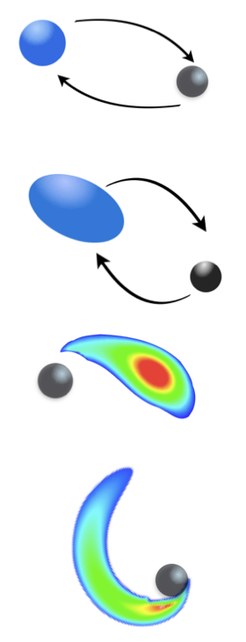
Grundlegende Einblicke in das Innere von Neutronensternen kann man aus Gravitationswellen bekommen, die beim Umlauf eines Neutronenstern-Binärsystems entstehen. Der Erfolg, diese Information zu erhalten, hängt jedoch von einem detaillierten Verständnis der Dynamik der Neutronensternmaterie und der Gravitationswellen-Emission ab. Wenn die beiden Objekte sich annähern, beginnt der Neutronenstern auf das Gezeitenfeld des Begleiters zu reagieren und verformt sich, ähnlich wie auf der Erde differentielle Gezeitenkräfte durch den Einfluss der Gravitation des Mondes entstehen. Für ein Doppelsystem aus einem Neutronenstern und einem Schwarzen Loch endet die Umkreisung, wenn der Neutronenstern in das schwarze Loch fällt oder wenn die Gezeitenkräfte des Schwarzen Lochs größer werden als die Eigengravitation des Neutronensterns und das Neutronensternmaterial sich zu einem Gezeiten-Schweif verformt. Für Systeme aus zwei Neutronensternen andererseits wird die Vereinigung durch die Hydrodynamik bestimmt. Die Details dieses Prozesses und die Identifizierung der charakteristischen Parameter, die das Gravitationswellensignal mit der Neutronenstern-Materie verbinden, bedürfen noch weiterer Aufklärung.

Mitglieder der Abteilung Astrophysikalische und Kosmologische Relativitätstheorie erweitern dieses Wissen, indem sie die gleichen analytischen Methoden verwenden wie bei Binärsystemen aus Schwarzen Löchern, und sie durch zusätzliche Berechnungen ergänzen, die die Komplexität der Materie beschreiben. Wir berechnen zum Beispiel die Reaktion der inneren Struktur eines Neutronensterns auf das äußere Gezeitenfeld in der Störungstheorie für verschiedene Modelle des Inneren des Neutronensterns. Da Neutronensterne Objekte mit starker Eigengravitation sind, muss dies in einem vollständig relativistischen Rahmen erfogen. Diese Berechnungen stellen eine direkte Verbindung zwischen der Neutronenstern-Mikrophysik und seinen globalen Eigenschaften wie den gezeiteninduzierten Multipolmomenten her. Um zu beschreiben, wie die Neutronensternstruktur die Zwei-Körper-Dynamik beeinflusst, entwickeln Forscher der Abteilung Astrophysikalische und Kosmologische Relativitätstheorie die Theorie der Gezeitenwechselwirkung innerhalb des PN-Rahmens, indem sie zusätzliche Einblicke in die Physik starker Felder im Testteilchen-Limit benutzen. Darüber hinaus formulieren und testen sie diese Resultate im Rahmen der EOB-Beschreibung, um das Modell bis zur Verschmelzung auszuweiten. Ein wichtiger Aspekt der Arbeit ist die Erstellung von Vorhersagen für die charakteristischen Parameter, die den Einfluss der NS-Materie auf die GWs beschreiben.

Die theoretische Arbeit der Abteilung befasst sich mit folgenden Fragen:

• Was sind effiziente Strategien, um das Zwei-Körper-Problem in der Allgemeinen Relativitätstheorie voranzubringen und weitere physikalische Effekte einzufügen? 
• Welchen Einfluss hat die Absorption Schwarzer Löcher auf Gravitationswellen?
• Was sind die beobachtbaren Eigenschaften der Spins Schwarzer Löcher, wenn sie sich gegenseitig und mit dem Bahndrehimpuls beeinflussen?
• Wie äußert sich die nichtkreisförmige Bewegung auf Gravitationswellen?
• Wie reagiert der Neutronenstern auf das Gezeitenfeld des Begleiters?
• Welchen Einfluss hat die zeitlich gestörte Neutronensternstruktur auf die Zwei-Körper-Bewegung?
• Was sind die wesentlichen Parameter, die den Einfluss der Neutronensternmaterie auf die Gravitationswellen beschreiben?
• Für Binärsysteme aus einem Neutronenstern und einem Schwarzen Loch: Welche Physik bestimmt die Frequenz der Gezeitenzerstörung?
• Für Binärsysteme aus zwei Neutronensternen: Werden Nichtlinearitäten vor der Verschmelzung wichtig?